ós sabemos que nem todas as pilhas de toras de madeira são perfeitas. Algumas toras podem ficar a frente ou atrás. Mas então, como a qualidade do empilhamento afeta as medições com o Timbeter?
Diâmetros individuais
Os objetos que estão mais próximos da câmera aparecerão maiores na imagem capturada. Isso significa que os diâmetros das toras que ficam a frente serão superestimados e as toras que estão atrás serão subestimadas. Mas quanto?

O tamanho de um objeto em uma dimensão da imagem é o resultado da seguinte fórmula:
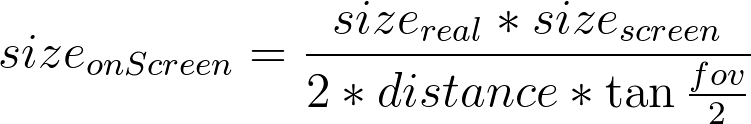
sizeonScreen – tamanho do objeto na imagem em pixels
sizereal – tamanho real do objeto
sizescreen – tamanho da imagem em pixels
distance – distância do objeto da câmera
fov – campo de visão da câmera
Assim como o tamanho da câmera do dispositivo, o campo de visão e o tamanho real das toras são constantes que não mudam quando nós nos movemos para mais perto ou mais longe. Então nós podemos simplificar a fórmula 1 para ver como uma tora que está a frente da pilha tem o seu tamanho afetado na medição:
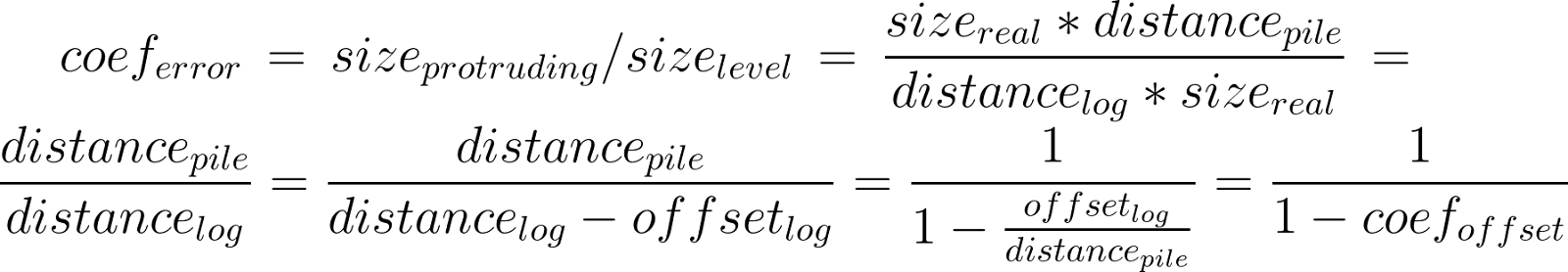
coeferror – proporção mostrando o quanto o objeto é superestimado
sizeprotruding – diâmetro da tora medida na imagem quando a tora está a frente
sizelevel – diâmetro da tora medida na imagem quando está nivelada
sizereal – diâmetro real da tora
distancepile – distância da câmera para a pilha
distancelog – distância da câmera para a tora
offsetlog – o quanto da tora está a frente da pilha
coefoffset – proporção mostrando o quanto da tora está a frente comparada à distância da pilha
A partir da fórmula, podemos ver que o diâmetro na imagem é inversamente proporcional à distância da câmera. Então, se uma tora está 2 vezes mais próxima de você, ela parecerá ser duas vezes maior. Por exemplo, se você capturar uma imagem à 2 metros da pilha e as toras estiverem 20 cm a frente da mesma, então o diâmetro será superestimado em 11.1%.
A fórmula também informa algo bastante útil: se nós queremos reduzir a margem de erro de diâmetros individuais, você pode simplesmente se afastar da pilha. Então, se uma tora está 20 cm a frente e você capturar a imagem estando 4 metros afastado, a superestimação será apenas 5.3%
Diâmetro médio
O resultado da medição do diâmetro médio é muito pouco afetado pela qualidade do empilhamento, levando em consideração que a qualidade da detecção não muda.
Vamos calcular o diâmetro médio de duas toras de 30 cm, quando a pilha está a 2 metros de distância e uma das toras está 20 cm a frente e uma 20 cm atrás:
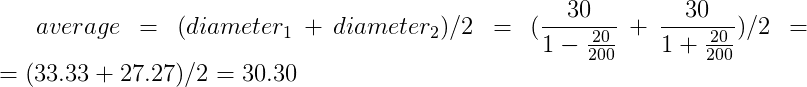
average – diâmetro
diameter1 – diâmetro da primeira tora na imagem
diameter2 – diâmetro da segunda tora na imagem
Como podemos ver, a média destas duas toras pode ser superestimada em 1%. Entretanto, isso ocorre apenas no caso das duas toras mais sobressalentes. A maioria das toras em uma pilha estarão muito mais próximas da média. Assumindo um posicionamento uniforme, nós podemos calcular o erro de diâmetro usando a seguinte fórmula:
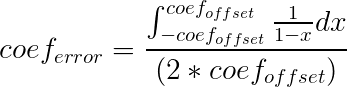
average – diâmetro médio na imagem
coef – proporção mostrando o quanto das toras sobressalentes estão compensadas no diâmetro médio da pilha se comparadas à distância
Em uma pilha que foi medida a 2 metros de distância e a toras são compensadas pela média da pilha em até 20 cm (o que significa que o coeficiente de compensação é 0.1), nós vemos que a superestimação é de apenas 0.34%. Além disso, se a imagem for feita com o dobro da distância, o erro será 4 vezes menor. No nosso caso, se uma imagem for tirada a 4 metros de distância, o diâmetro médio será superestimado em apenas 0.083%.
Volume da pilha
Pilhas irregulares afetam o volume medido mais do que o diâmetro médio, mas o efeito ainda sim é bastante limitado. Eles são diferentes porque nós precisamos multiplicar o diâmetro para calcular a área de superfície da tora e o volume, o qual muda a proporção entre os dois valores.
Para computar o erro na medição do volume de uma pilha irregular, nós usamos a seguinte fórmula:
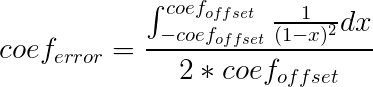
coeferror – proporção mostrando o quanto do volume é superestimado
coefoffset – proporção mostrando o quanto das toras sobressalentes são balanceadas na média da pilha comparadas à distância da câmera
Nós descobrimos que se você estiver a 2 metros da pilha e as toras estiverem adentro ou a frente numa média de 20 cm, então o volume médio será superestimado em 1%.
Novamente, ao se distanciar 2 vezes mais da imagem a ser capturadas, o efeito será o mesmo de tornar a pilha irregular pela metade, o que reduz o erro em 4 vezes. Se a pilha for capturada a 4 metros de distância, então o volume será superestimado em 0.25%.
Conclusões
O quanto a qualidade da pilha afeta uma medição depende muito do que está sendo medido. Diâmetros individuais são muito sensíveis à qualidade do empilhamento, mas você pode ignorar este fato se você estiver medindo o diâmetro médio. Para a medição de volume, a maioria dos nossos usuários nota que as medições são muito precisas. Entretanto, se as suas pilhas forem irregulares ou se você tirar fotos muito próximo a elas, você deve considerar como isso pode afetar os seus resultados. Lembre-se, se você quer reduzir a quantidade de erros produzidos por um mau empilhamento, você sempre pode fazer a medição a partir de uma distância maior.
